Chapter Objectives

  • Display data graphically and interpret the following graphs: stem-and-leaf plots, line graphs, bar graphs, frequency polygons, time series graphs, histograms, box plots, and dot plots
  • Recognize, describe, and calculate the measures of location of data with quartiles and percentiles
  • Recognize, describe, and calculate the measures of the center of data with mean, median, and mode
  • Recognize, describe, and calculate the measures of the spread of data with variance, standard deviation, and range

Assignment

Data Spread

  • Mean can tell you where the data is
  • Spread can tell you how concentrated it is at the center
  • Standard deviation measures the spread of data from the mean
  • This spread is also called variation

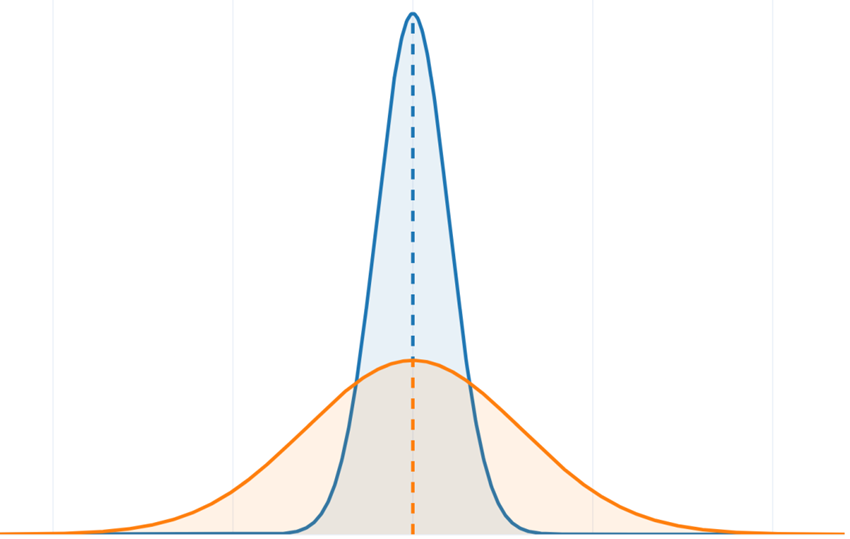
Figure 2.7.1 The orange distribution has a much higher variance than the blue distribution.

Standard Deviation as a Ruler

  • A set of data has a mean of 80 and a standard deviation of 5
  • A value of 85 is one standard deviation above the mean. 75 is one below. 90 would be two standard deviations.
  • How many is 88?

Z-scores

Where $x$ is the value, $\mu$ the mean, and $\sigma$ the standard deviation,

\[\begin{align} z &= \frac{x - \mu}{\sigma} \end{align}\]
  • Z-scores tell you how many standard deviations a data point is from the mean
  • Positive is above, negative below
  • 88 has a z-score of $(88−80)/5=1.6$, so 1.6 standard deviations above the mean
  • 67 has a z-score of $(67−80)/5=−2.6$, or 2.6 standard deviations below the mean

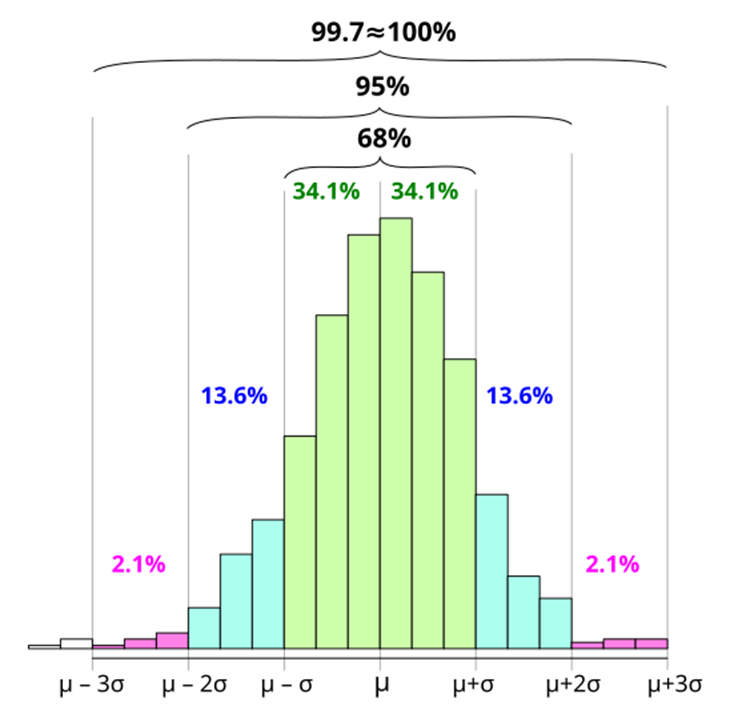
The Empirical Rule (68-95-99.7 Rule)

  • A normal distribution where the bulk of the data is in the middle
    • 68% of the data falls within one standard deviation
    • 95% falls within two
    • 99.7% falls within three

Figure 2.7.2 A visual representation of the Empirical Rule.

Calculating Standard Deviation

Standard Deviation

Where $x$ represent each data value, $\mu$ the mean, and $n$ the total number of values,

\[\begin{align} \sigma &= \sqrt{\frac{\sum (x - \mu)^2}{n}} \end{align}\]

In other words,

  1. Find the differences between each data point and the mean
  2. Square each one
  3. Add them all up
  4. Divide by the number of data points
  5. Square root that quotient

Standard Deviation vs IQR

  • Mean and standard deviation are related
  • Median and IQR are also related
  • First measures the center, second the spread
  • Mean and standard deviation are influenced by the magnitude
  • Median and IQR care only about position